nlcpy.random.Generator.standard_gamma
- Generator.standard_gamma(self, shape, size=None, dtype='d', out=None)
Draws samples from a standard Gamma distribution.
Samples are drawn from a Gamma distribution with specified parameters,shape (sometimes designated "k") and scale=1.
- Parameters
- shapefloat
Parameter, must be non-negative.
- sizeint or tuple of ints, optional
Output shape. If the given shape is, e.g.,
(m, n, k), thenm * n * ksamples are drawn.- dtypestr or dtype, optional
Desired dtype of the result, either 'd' (or 'float64') or 'f' (or 'float32'). All dtypes are determined by their name. The default value is 'd'.
- outndarray, optional
Alternative output array in which to place the result. If size is not None, it must have the same shape as the provided size and must match the type of the output values.
- Returns
- outndarray
Drawn samples from the parameterized standard gamma distribution.
注釈
The probability density for the Gamma distribution is
where
is the shape and
the scale, and
is the Gamma function.
The Gamma distribution is often used to model the times to failure of electronic components, and arises naturally in processes for which the waiting times between Poisson distributed events are relevant.
制限事項
If shape is neither a scalar nor None : NotImplementedError occurs.
Examples
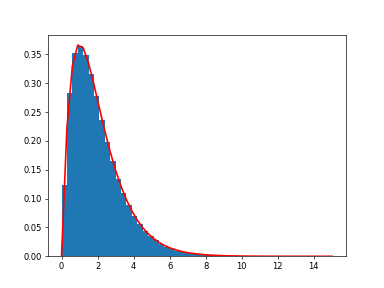
Draw samples from the distribution.
>>> import nlcpy as vp >>> shape, scale = 2., 1. # mean and width >>> s = vp.random.default_rng().standard_gamma(shape, 1000000) >>> import matplotlib.pyplot as plt >>> import scipy.special as sps >>> count, bins, ignored = plt.hist(s.get(), 50, density=True) >>> y = bins**(shape-1) * ((vp.exp(-bins/scale))/ ... (sps.gamma(shape) * scale**shape)) >>> plt.plot(bins, y, linewidth=2, color='r') >>> plt.show()